引言
上面是一颗橡树,枝繁叶茂,我们也常用枝繁叶茂来形容一个家族枝繁叶茂,原因在于树和家族之间具备共性,都是从根向外延伸,我们将树倒过来看可能体会更深一点:

如果我们我们目前主干算做根的一部分,或者说他们本就是一部分,只看枝干,那么树就可以转换为一个家族:
除了家族是一种树形结构,图书馆的分类我们也可以看做是一种树形结构,我们进入图书馆找书的时候,会先确认这本书属于哪一个分类,根据分类去对应的楼层,再根据楼层再去找他的小分类,图书馆的分类也是一种树形结构:
除此之外还有组织架构、计算机的目录结构等都属于树形结构,由此我们也就是引出了数据结构中的树。从上面的例子我们可以看出,当数据元素之间呈现的关系非一一对应,对应的关系复杂之后,线性数据结构应对这种类型的数据结构是力不从心的,我们需要一种符合树形结构特点的其他方式来描述这种呈层次关系的非线性结构。
数据结构中的树
树的基本定义和基本术语
树(tree)是包含n个结点的有限集合,其中:
有一个特定结点被称为根结点或根,他只有直接后继,但没有直接前驱。 除根结点之外的其余数据元素被分为m(m >= 0)个互不相交的集合T1,T2,...,Tm,其中,每一个集合Ti( 1 <= i <= m)本身也是一颗树,称为根的子树。
当树的集合为空时,n =0,此时称为空树,空树没有结点。
树是递归结构-在树的定义中又用到了树的定义,一颗非空树是由若干子树构成的,而子树又可以由更小的子树构成。
树的特点
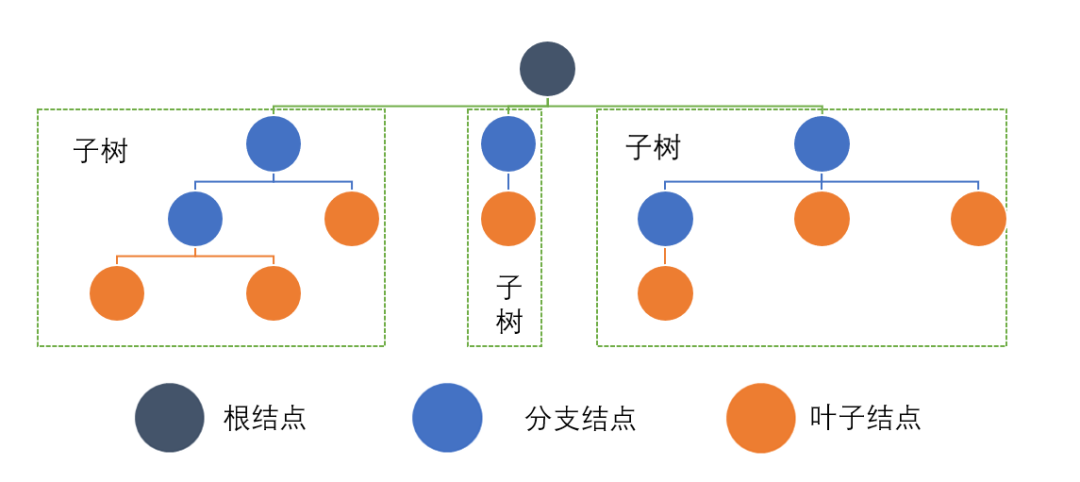
如上图所示:
每个结点都有零个或多个子结点,无子结点的结点被称为叶子结点。 没有父节点的结点被称为“根结点”,规定它所在的一层为第一层。 每一个非根结点有且只有一个父结点。
树常用术语的介绍
(1) 树的结点: 包含一个数据元素, 可以同时记录若干指向子树分支信息。
(2) 孩子(child) 和 父亲(parent)
种某个结点的子树之根被称为该结点的孩子或儿子,相应地,该结点称为孩子的双亲,同一个双亲的孩子被称为兄弟。
(3) 祖先(Ancestor)和子孙(Descendant)
若树中存在一个结点序列k1,k2,...,ki,...,kj使得ki是ki+1的双亲(1<=i<=j),则称该结点序列及其上的分支是从k1到kj的一条路径和道路。
路径的长度指路径所经过的边(即连接两个结点的线段)的数目,等于j - 1. 从树的根结点到树中其余结点存在一条唯一路径。
祖先和子孙: 若树中结点k到ks存在一条路径,则称k是ks的祖先,则称k是ks的祖先,ks是k的子孙。
一个结点的祖先是从根结点到该结点的路径上所经过的所有结点,而一个结点的子孙则是以该结点为根的子树中的所有结点。
约定: 结点k的祖先和子孙不包含结点k本身。
(3.1) 结点的层数(Level)和树的高度(Height)
结点的层数从根起算: 根的层数为1.其余结点的层数的等于其双亲结点的层数加1。双亲在同一层的结点互为堂兄弟。
树中结点的最大层数称为树的高度或深度。
注意,也有文献中将树根的层数定义为0。
(3.2) 结点的度(Degree)
树中的一个结点拥有的子树个数称为该结点的度。一颗树的度是指该树的结点的最大度数。下面这棵树的度就是3:
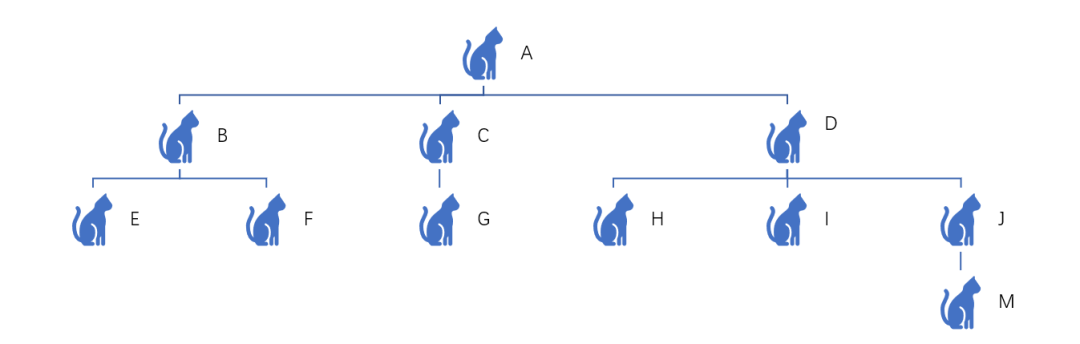
度为零的结点称为叶子(Leaf)或终端结点。度不为零的结点称为分支结点或非终端结点。度不为零的结点称分支结点或非终端结点。除根结点之外的分支结点称为内部结点。根结点又被称为开始结点。
(3.3) 有序树(OrderedTree)和无序树(UnorderedTree)
若将树中每个结点的各个子树看成从左右有次序的(即不能互换),则称该树为有序树,否则称为无序树。
注意:若不特别指明,一般讨论的树都是有序树。
(3.4) 森林(Forest)
森林是m(m >= 0)棵互不相交的树的集合。
树和森林是相关的,删去一颗树的根,就得到一个森林;反之,加上一个结点作为树根, 森林就变为一颗树。
树的逻辑结构特征
树形结构的逻辑特征可用树中结点之间的父子关系来描述。
(1) 树中的任一结点都可以有零个或多个直接后继(即孩子)结点,但至多只能有一个直接前驱(即双亲)结点。
(2) 树中只有根结点无前驱,它是开始结点,叶节点无后继,它们是终端结点。
(3) 祖先与子孙的关系是对父子关系的延拓, 它定义了树中结点之间的纵向次序。
(4) 有序树中,同一组兄弟结点从左到右有长幼之分。
对这一关系加以延拓,规定若k1和k2是兄弟,且k1在k2的左边,则k1的任一子孙都在k2的任一子孙的左边,那么就树中结点之间的横向次序。
树的存储结构
树形结构的存储,依然要遵循存储的两大原则:
“存数值、存联系” “存得进、取的出”
由于树是非线性结构,结点间的联系的存储,要比线性结构复杂的多,根据树形结构的特点,每个结点与其直接相连的结点关系只有两类,一是双亲,二是孩子。对于一个结点而言,其双亲只有一个,孩子可以有0到n个。树形结构的存储结构设计原则,即是要实现双亲、孩子关系如何直接或间接存储。对于设计好的存储结构标准则是只要在存结构中能找到一个结点的这两种存储关系,那么这样的存储结构设计就是可行的。我们可以称之为“双亲孩子检验原则”。
同样的树的存储结构也有两种存储方式, 连续存储方式和链式存储方式。
树的连续存储方式
双亲孩子表示法
按照“存数值,存联系”的原则,用数组存储树中结点的值,对应有下标,即结点的编号,则每个结点的双亲与孩子通过这个编号,就可以标示出来

如上图用数组来标示就下面所示:
| 下标 | 结点数据 | 双亲位置 | 孩子位置 |
|---|---|---|---|
| 0 | A | -1 | 1,2,3 |
| 1 | B | 0 | 4,5 |
| 2 | C | 0 | 6 |
| 3 | D | 0 | 7,8,9 |
| 4 | E | 1 | -1 |
| 5 | F | 1 | -1 |
| 6 | G | 2 | -1 |
代码示例:
// 这里我们先只给出一个大概的结点结构。
public class ArrayTree<T> {
private int parentIndex;
private int[] children;
private T t;
public ArrayTree() {
}
public int getParentIndex() {
return parentIndex;
}
public void setParentIndex(int parentIndex) {
this.parentIndex = parentIndex;
}
public int[] getChildren() {
return children;
}
public void setChildren(int[] children) {
this.children = children;
}
public T getT() {
return t;
}
public void setT(T t) {
this.t = t;
}
}
双亲表示法
树形结构的特点是每个结点的双亲是唯一的,我们可以从结点的是双亲关系间接得到孩子的信息,所以我们也可以只存储双亲的位置,就可以得到结点的双亲及孩子信息,所以树的连续存储方式可以简化为下面:
public class ArraySimpleTree<T>{
private int parentIndex;
private T t;
public ArraySimpleTree() {
}
public int getParentIndex() {
return parentIndex;
}
public void setParentIndex(int parentIndex) {
this.parentIndex = parentIndex;
}
public T getT() {
return t;
}
public void setT(T t) {
this.t = t;
}
}
孩子表示法
public class ArrayChildrenTree<T> {
private int[] children;
private T t;
public ArrayChildrenTree() {
}
public int[] getChildren() {
return children;
}
public void setChildren(int[] children) {
this.children = children;
}
public T getT() {
return t;
}
public void setT(T t) {
this.t = t;
}
}
树的链式存储方式
用链表来构建树,线性链表的前驱和后继各有一个,因此线性链表存储形成的链也是直的一条,你可以理解为这个家族都是单传,那么将后继改为多个就变成了树。
孩子表示法
public class LinkedTreeNode<T> {
private T data;
private List<LinkedTreeNode> nodes;
public LinkedTreeNode() {
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public List<LinkedTreeNode> getNodes() {
return nodes;
}
public void setNodes(List<LinkedTreeNode> nodes) {
this.nodes = nodes;
}
}
孩子兄弟表示法
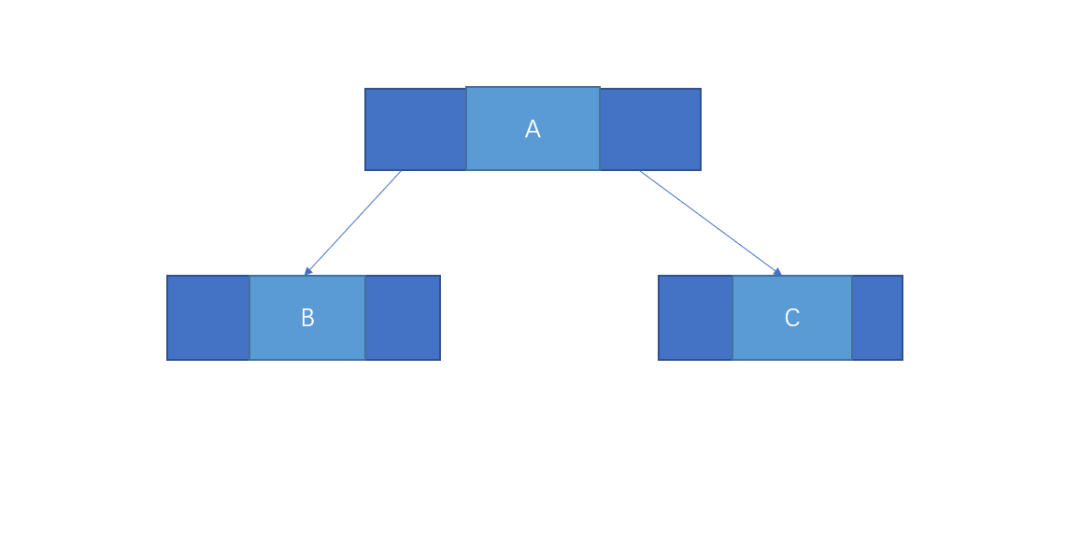
在存储树中每个结点时,除了包含该结点值域外,还设置两个指针域分别指向该结点的第一个孩子结点和其右兄弟,即最多只记录两个孩子的信息,这样就可以用一种统一的二叉链表的方式加以存储,因此该方法也常被称为二叉树表示法。
这种存储结构易于实现找结点孩子的等的操作,找结点的双亲不易。
public class BinaryTreeNode<T> {
private T data;
private BinaryTreeNode rightNode;
private BinaryTreeNode leftNode;
}
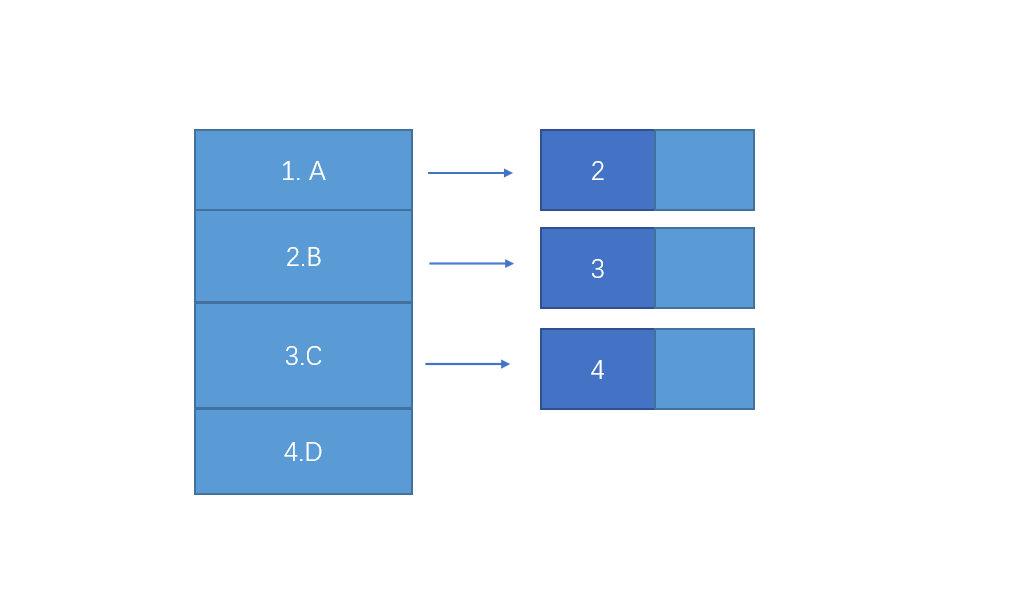
树的链式存储--孩子链表表示法
此法是树的连续存储与链式存储的组合存储方式,把每个结点的孩子结点排列起来,看成一个线性表,且以单链表为存储结构,则n个结点有n个孩子链表(叶子的孩子链表为空表)。如下图所示:
public class SequenceTree<T> {
private LinkedListNode<T> nodeList;
private T data;
private class LinkedListNode<T> {
private T value;
private LinkedListNode<T> next;
}
}
总结
在写树这一节的时候,不想堆砌太多概念,想追随的是《C语言程序设计现代方法》的风格,在讲述每一节的时候只讲必要的概念,不堆砌,用的时候才铺陈概念,但是实践这一点似乎比较难,因为你需要对这个知识有足够了解,才能做到如此的游刃有余。但我们是无法一下子做到完美的,如果我像这样去写作,恐怕这篇文章永远发不出来。等到之后对数据结构比较熟悉之后,这部分的文章也许会重构一下。
参考资料
·《数据结构与算法分析新视角》 周幸妮 任智源 马彦卓 樊凯







